Spicing up rocketing with the launch of some multiple stage model rockets.

A model rocket has a typical launch sequence. Understanding this will help one to choose a proper launch site. Google maps can help you determine your launch site dimension that you can use to help choose the best engine size for your launch area.

A video created as inspiration to model rocketry...#JROspace

Early morning launch tests on new designs and adjustments on some model rocket cars. #JROspace

Launching model rocket cars in the park. #JROspace

Although ending the run with a crash, enough data was available to determine the speed of the car before the crash. #JROspace

A rocket based on the Estest V2 model rocket. #JROspace

A homemade Sh*t model rocket, the Honey Badger III, and the Alligator Gar model rockets launch again. #JROspace

Launching the Estes Rascal model rocket near Densmore, KS, on Memorial Day. #JROspace

An Estes Big Daddy model rocket launches near Densmore, KS, on Memorial Day, 2017. #JROspace

A homemade two stage model rocket that was recovered from a lake two weeks before. #JROspace

Launching ready to fly Estes rockets of Rascal and HiJinks....lost the HiJinks. #JROspace.

A video provided to teachers who are interested in using model rockets in their classroom but might need some help getting started.

Bored of mathematics? Tired of teaching math? Bored out of your mind? I have a few ideas to spice things up. #JROspace
http://johnrozean.wix.com/mysite

Agni-V is an intercontinental ballistic missile developed by the Defense Research & Development Organisation (DRDO) of India. Agni V is part of the Agni series of missiles operated by the Indian military. Agni V is a missile thought to have a range of 5,500 to 5,800 km. #JROSpace

Model rocket car races. #JROspace

Model Rocket car crash. #JROspace

Tight conditions on a windy day....A friend gets a souvenir. #JROSpace

Very windy day...kind of tight conditions. This homemade rocket lands in a lake. #JROSpace

An Easter tribute music video showcasing model rocketry.

Easter Sunday, 2017. In honor of the freedoms of the First Amendment -- specifically, religion -- this video offers up insight and some cool model rocket launches.

Story of a treasured model rocket recovered.

Obsessed with clustering of rocket engines, and the saber rattling between Trump and Kim, we decided to do a reckless launch ourselves.

After three crashes, a fire, and three rebuilds, I finally got a successful launch with this home-designed rocket. Pretty happy about this one.
335 g at launch, 92 cm in length. Estes E12-6 engine.

What's this item about? What makes it interesting? Write a catchy description to grab your audience's attention...

What's this item about? What makes it interesting? Write a catchy description to grab your audience's attention...

First launch of the Athena rocket....Estes Part 2452....

For the sake of education, I figured that I would try out some totally air-powered rockets. These things will surprise you!

Using video software as a means to calculate the speed of a toy rocket car

Focused on getting video of the process of a rocket car. While I am trying to develop a cordless model, this model operates on a chord as standard Estes cars do with some minor modifications to the kit. This video will be used in a later video to calculate the speed of this toy rocket car.

CSI 135 does something weird. A completely homemade sh**t rocket steals the show..a little talk radio style banter about fake news....FREEDOM 2

The smoke settles during a still, early morning launch with temperatures hovering around freezing. Attempting to get the space man to eject from the Estes Free FallFall to no avail. Also featured are the Crossfire, Alpha II, and the Custom Freedom rockets.

Focus on recovery of homemade model rocket. Use of C6-0 engine

Homemade model rocket with E12-6 engine. 

This is the third time this prototype has been rebuilt. The first occasion called for restructuring of the wings, the second involved adding three minor wings, however the rocket engine appeared to fail causing a fire that left a great deal of the rocket inoperable; resulting in a new nomenclature for the rocket as a II generation of the rocket. This was the first time the rocket was able to get off the ground with considerable stability; however, the recovery ejection resulted in a loss of the parachute and a hard landing. Works are already in place for a Honey Badger III, which will entail a larger diameter tube being added while the lower half of the rocket remains generally intact.

The Honey Badger series has been plagued with bad luck -- some due to design, some just the luck of the draw. J-Ro has great hopes for this model and has further plans for the model rocket series.
 

A three stage rocket captured on video....with engines B6-0, B6-0, & C6-5.

The physical trajectory is due to two individual forces: the force with which the object is shot and the force of gravity. The force with which the object is shot gives it an initial speed and a direction. The initial upward-angled velocity of the object "fights" with the acceleration of its fall. The outcome is a smooth curve called a parabola. This position function can be determined by taking data of the position of the object and using technology to get the function's equation.

Lift off: SpaceX's Falcon 9 rocket lifts off from Launch Complex 39A - the same spot from which astronauts flew to the moon 48 years ago  - on Sunday, carrying 5,000 pounds of supplies to astronauts on the ISS. It landed again after the mission

Read more: http://www.dailymail.co.uk/news/article-4240876/Incredible-moment-SpaceX-rocket-lands-launch-pad.html#ixzz4ZGEMJz9e 
Follow us: @MailOnline on Twitter | DailyMail on Facebook

Launch from Columbia, MO, 12 FEB 2016 set to music with creative license allowed. Sun setting as the launch sequence progresses. Featured are the Commanche III stage rocket, the homemade Dewsky I, and the Agni 5 nuclear missile replica.

The height of a model rocket can be calculated using the angle of elevation from a know point on the ground. An Estes Altitrack is designed specifically for this. Estes Educator.com offers up various lesson plans that incorporate model rocketry to the classroom. This is one of those lessons related to 3-5 grade mathematics.

Couple of early morning launches at the old tree in Columbia, MO. The SF-15 North Korean replica ends up doing a nose dive into the earth.

Trying out a homemade E class engine type....

Me communicating in Xarconian on my grandfather's organ and a paint in the launch tube oversight.

Homemade design alien craft...good test run...

My first experience with E class type engines. From experience with most C-engine type rockets, I kinda know how to angle the launch pad to play the wind. The angle proved accurate from the C-engine type rockets, however since E class type engines have a 33 percent more powerful total impulse. Well, now I know.

I had been bragging about the height that this pop bottle would get off this water launcher all night and most of the day. So the buildup may have gone a bit too far. But, I knew that I had set the bar a bit high. Maybe? The problem was I suddenly forgot the measurements that I had had during that bragged, successful launch. Nevertheless, the pressure was on.

Stretching out the legs….I was maxing out the engines on all the rockets. Trying to get some air time. My dad and friends came out to watch the air show.

J-RO space near vanished. With the CEO’s absence due to health conditions, the sinister J-RO has risen from the ashes to try to breath new life into the organization.

Estes Rocket fired in a strip mall parking lot...Couple crash and burns

"In this Brainfoo project I wanted to revisit a childhood favourite and create the best match rocket I could. Fellow mini rocketeers on the internet had claimed to achieve  a distance of up to 40 feet, which is better than the 20 – 30 feet I remember as a teenager. The real question was how far could I take it when approaching it with an adult brain?"

Rockets Launched
-1/2 Gen. E2X (Orange)
Estetes Gen E2X (green/red)
Alpha red
Alpha Black
Bandit 3
Bandit 1
Alpha III...

Had a little troube with my Mercury class rocket.....

Rockets launched..

Dominos Rewards

Bandit 2

Alpha (modified)

​

w/ slow motion effects

Launch sequence. 2 camera angles. After Action Review;

Rockets Launched

Amazon

High Flyer

Yankee

Crossfire

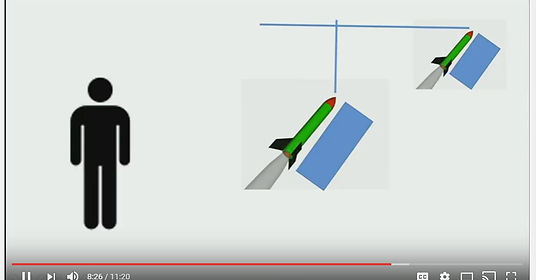
Calculating a rockets Speed

ROZEAN:

So far in this presentation we have discussed three things, Measurement, Geometry and rocketry. In the following minutes we are going to bring all those things together. During the launch sequence, two camera angles were used to gather information about our rockets. We are going to focus on the Amazon rocket.

ROZEAN:
More specifically, we are to use the elements of measurement, such as distance, and the Geometric elements and triangles to determine a relationship between distance and time, which we call speed. As you can see I am using a combination of the program PowerPoint and captured video stills to measure the distance travel by the rocket in a fraction of a second. When I click on the rectangle, PowerPoint will give me its measurement in inches.

ROZEAN:
I measured the height of the rocket Amazon in the same manner as you can see the measurements are given in the video. I also measured the real rocket so that a proportion can be made between the video and reality. The Amazon rocket was 74 cm. Now to complete our relationship, so that we can calculate rate, more commonly known as speed, we also needed a time increment. Luckily the video program that I have measures time up to the ten-thousandths place.  And there you see the two time readings. Now we can need to simply subtract those two time readings to calculate the time interval of which we measured, which is a fraction of a second.

ROZEAN:

Measurement of the rocket is going to be a little bit off. Because remember the rocket was moving at an angle. And it was moving away from us. So overtime its view is going to be slightly distorted. So we can use this distortion as a proportion to get a better calculation of rate or speed. As demonstrate in this graphic, as the rocket moves through the camera lens, it appears to get smaller. But using the measurements through power point and our knowledge of proportionality, we can adjust for this. This proportion or ratio is graphically demonstrated as a right triangle. As we play with this proportion, our triangle begins to look like a 30-60-90 triangle. Actually, using a little Trigonometry, it’s about a 18-72-90 triangle; but we are going to use the 30-60-90 triangle for simplicity.

ROZEAN:
Now we need to do some calculations, if you remember, our PowerPoint distance traveled was 2.31 inches, and our PowerPoint rocket was 1.23 inches. In the actual measurement of the Amazon rocket that I measure, it was 74 cm. Now we need to solve for some unknowns. The best way to do this is to set up a proportion equation and solve for the unknowns using Algebra. So here is our ratio, the PowerPoint distance traveled, divided by the PowerPoint height of the rocket. That will be set to equal the distance traveled in reality over the actual height of the rocket, which was 74 cm.

ROZEAN:

Now we are just going to solve for x, what we do is cross multiply by 74 to get the unknown distance traveled. Our first step is the divide 2.31 by 1.23 and we 1.8780. Now we are going to multiply that times 74 and we get about 139 cm. Model rocket speed is usually measured in feet per second. And if you remember 1 inch is equal to 2.54 cm. So if we divide 139 by 2.54 and we get about 55 inches. Now to convert that into feet we divide that by 12, and we get about 4 and a half feet in that very small time frame. Remember that that small time frame was 0.124 seconds. So we divide out distance traveled by .124. So we get about 37 feet per second. So how does this translate into something that we better understand such as miles per hour. Here is the standard conversion. 1 foot per second is 0.68 miles per hour. So we multiple our foot per second times 0.68, yielding 25 mph

ROZEAN:

That is a great calculation, we are actually not measuring the distance traveled by the rocket, we are measuring the vertical distance. We want to measure the hypotenuse of that triangle as that in red. So as we said, when we drew that proportion over the varying sizes of the rocket, we were able to find a proportion ratio, which was about a 19-71-90 triangle but we are going to assume that it is 30-60-90 triangle for simplicity, so we are going to have to use the special triangle theorem. What we calculated was actually the short leg of the right triangle. So the short leg is 4.56 feet long. And the hypotenuse, the actual distance traveled by the rocket is actually 2 times that. So we multiply 2 times 4.56. And we get 9.12 feet. Now we got to divide that by the time increment to get our speed, and that increment yields about 76 feet per second. And we want to convert that to miles per hour, we multiple by 0.68 and that yields about 50 miles per hour.

ROZEAN:
These were rough calculations, but they do make sense for a larger rocket like the Amazon coming right off the launch pad. Rocket speed is always increasing as long as the engine is burning. As you can see from this estes graph. So the initial speeds may be lower than the top speed just before the parachute is deployed.